כיצד לפתור את המשוואה הריבועית

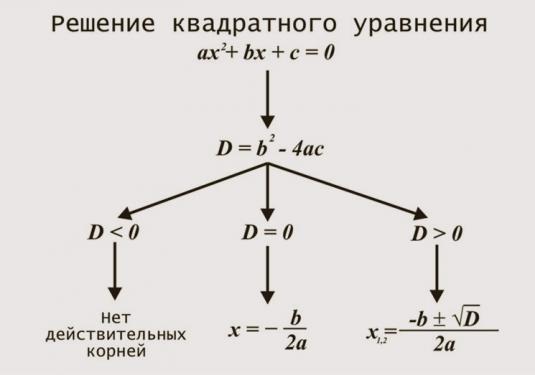
משוואה ריבועית מלאה נפתרת על ידי מציאת שלה מפלה.

נזכיר כי משוואה ריבועית מלאה היא משוואה של rx הטופס²+ wx + h = 0, כאשר r, w, h הם המקדמים של המשוואה הריבועית: מספרים מסוימים אינם שווים לאפס, ו- x הוא משתנה (לא ידוע).

כיצד לפתור את משוואת ריבוע דרך המפלה

לחשב את discriminant (D) של משוואה ריבועית. כדי לחשב את המפלה, לחסר את התוצר של המקדמים r ו- h ב -4 מהמקדם השני w, שהועלה למקור השני.

D = w²- 4rh

אם המפלה המתקבלת של המשוואה הריבועית היא פחות מאפס (D <0), אזי למשוואה זו אין שורשים, ולכן אין לה פתרון.

אם וכתוצאה מכך מפלה של ריבועהמשוואה היא אפס (D = 0), אז למשוואה יש רק שורש אחד. כדי לחשב את השורש הזה, יש לחלק את מקדם המשוואה הריבועית w עם סימן החיסור על ידי פעמיים במקדם r.

זוהי הנוסחה למציאת שורש יחיד:
x = -w / 2r

אם המבחין של המשוואה הריבועית גדול מאפס (D> 0), אז שני שורשים ניגשים למשוואה.

כדי למצוא את השורש הראשון של משוואה ריבועית x₁, יש להוסיף את השורש הריבועי של המפלה למקדם w עם סימן מינוס, ולחלק את התוצאה פעמיים במקדם r.

כדי למצוא את השורש השני של המשוואה x₂, יש לחסר את השורש הריבועי של המפלה מן המקדם w עם סימן מינוס, ולחלק את התוצאה על ידי פעמיים מקדם r.

אם משוואה ריבועית מלאה של rx הטופס²+ wx + h = 0 הוא מופחת, כלומר, המקדם ליד הלא ידוע הכוח השני שווה לאחדות (r = 1), אז אפשר לפתור את זה על ידי הנוסחה של משפט וייט.

כיצד לפתור את משוואה ריבועית מופחתת באמצעות הנוסחה של משפט וייטאה

משפט וייט הוא כדלקמן: סכום השורשים של המשוואה הריבועית המופחתת שווה למקדם השני, רק עם סימן ההפך, ותוצר השורשים שווה למושג החופשי.

כלומר, אם משוואה של הטופס rx²+ wx + h = 0 יש שורשים אמיתיים, לאחר מכן

• x₁ + x₂ = -ww
• x₁ * x₂ = h

מ נוסחאות אלה אפשר לנסות לנחש את שורשי המשוואה. לשם כך, אנחנו צריכים להרחיב את טווח חופשי H לשני גורמים, סכום אשר יהיה שווה מקדם w עם סימן ההפך.

לדוגמה

אנו לוקחים את המשוואה הקטינה x²- 8x + 12 = 0

אנו יודעים כי:

• x₁ + x₂ = 8
• x₁ * x₂ = 12

אנחנו צריכים לפרק 12 לתוך שני גורמים כאלה, אשר יחד לתת 8. ברור כי 6 ו 2 הם גורמים כאלה.

ואכן:

• 6 * 2 = 12
• 6 + 2 = 8

מכאן נובע כי המספרים 6 ו -2 נכוניםשורשים עבור משוואה ריבועית מופחתת. פתרונות ברורים כאלה מגיעים במהירות לראש כאשר עובדים עם מקדמים שלמים פשוטים של משוואה ריבועית. לכן, משפט ויאטה משמש לעתים קרובות לבחירת שורשי משוואות ריבועיות, מה שחוסך זמן רב בפתרון אותן.