איך למצוא את הזוויות של משולש?

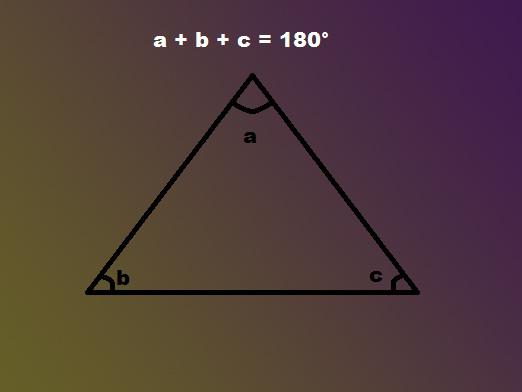
קרוב לוודאי שכולם יודעים דמות כה פשוטה,המורכב משלושה קווים מחוברים, כמו משולש. מתוכנית בית הספר עדיין ידוע לכולם איך למצוא את הצדדים של המשולש, אבל היום כמה אנשים זוכרים את הכללים האמיתיים ואת הנוסחאות. וגם לרענן את זה בזיכרון, זה לא יזיק בכלל, כי לפעמים זה פשוט צריך לדעת את הכללים איך למצוא זוויות במשולש על מנת לקבוע מרחק מסוים בחיי היומיום.

בואו ננסה לזכור את משפט פיתגורס,אשר מציין כי הריבוע של hypotenuse שווה לסכום של הריבועים של שתי הרגליים. אנו מתייחסים הצדדים של משולש כמו crosspieces כי מצטלבים בזווית של 90 מעלות. Hypotenuse הוא הצד ביניהם. לדעת את אורך של שני הצדדים, אתה יכול לחשב את השלישי של הנוסחה.

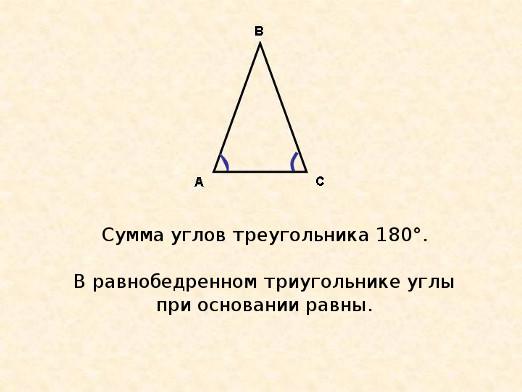
ישנם עוד כמה כללים, איך למצוא את השלישיזווית של משולש, אבל אלה משפטים קצת יותר מסובך. בהמשכו של משפט הסינוס, הצדדים של המשולש הם פרופורציונליים כדי sine של זוויות מנוגדות. כלומר, יש נוסחה לפיה רדיוס המעגל מוגבל על משולש, מוכפל בשניים, שווה ליחס של כל צד של המשולש אל הסינוס של הזווית ההפוכה. לדעת את הנתונים, אתה יכול לחשב את הצדדים החסרים. אפשר גם לפנות משפט הקוסינוס, אשר generalizes את המשפט מאוד של פיתגורס. הריבוע של צד אחד שווה לסכום הריבועים של שני האחרים, למעט את התוצר הכפול של הצדדים האלה על ידי הקוסינוס של הזווית ביניהם.

החשוב ביותר מכל נוסחאות אלה הוא להיות מסוגל להחליף כראוי את הנתונים ולמצוא את הלא ידוע, שכן גזירה לא נכונה של הלא ידוע לא ייתן את התוצאה הנכונה.