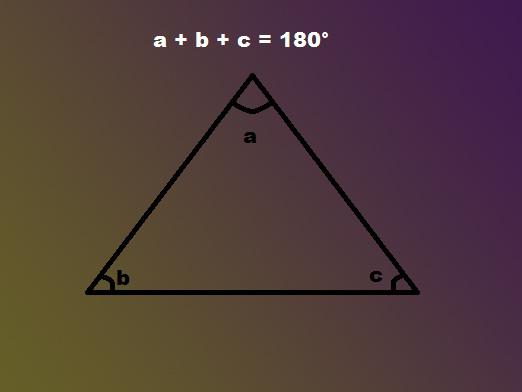
מאפיינים של משולש איסוסל

משולש ששני צדדיו שווים ביניהםנקרא משקפיים. צדדים אלה נקראים לרוחב, והצד השלישי נקרא הבסיס. במאמר זה, נוכל לספר לך על המאפיינים של משולש משקפיים.

משפט 1

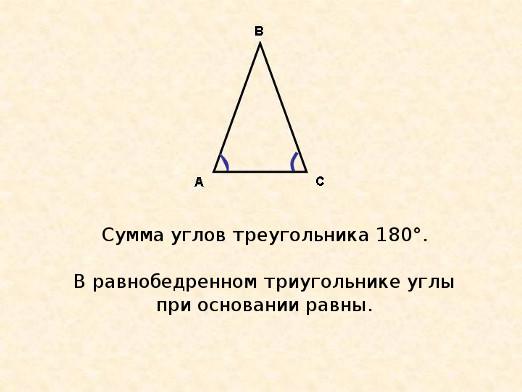
זוויות ליד הבסיס של משולש isosceles שווים אחד לשני

הוכחת המשפט.

נניח שיש לנו משולש משקפייםABC, שבסיסם AB. בואו נסתכל על BAC המשולש. משולשים אלו, השורות הראשונות, הם שווים. זהו, אחרי הכל לפנה"ס = AC, AC = BC, זווית ACB = ACB זווית. מכאן נובע כי הזווית = BAC זווית ABC, זה הזוויות המקבילות שלנו שווות לכל משולשים אחרים. הנה לך ואת הזוויות של נכס משולש שווה שוקיים.

משפט 2

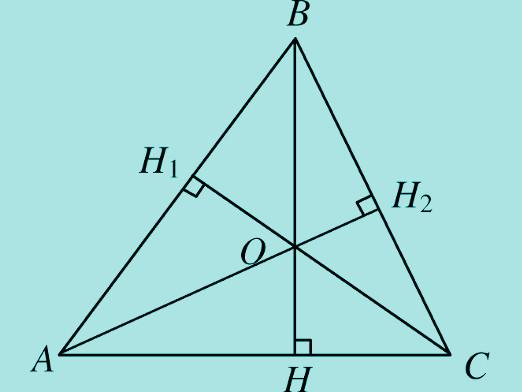
החציון במשולש השוליים, שנשא לבסיס שלו, הוא גם גובה וביסקטריקס

הוכחת המשפט.

נניח שיש לנו משולש משקפייםABC, שבסיסה הוא AB, ו CD הוא חציון שערכנו לבסיס שלה. ב משולשים ACD ו BCD, זווית CAD = זווית CBD, כמו זוויות המקביל בבסיס משולש isosceles (משפט 1). ואת הצד AC = צד לפנה"ס (על ידי הגדרת משולש משקפיים). צד AD = צד BD, לאחר נקודה D מחלק את קטע AB לחלקים שווים. משמעות הדבר היא כי משולש ACD = משולש BCD.

מן השוויון של משולשים אלה יש לנושוויון הפינות. כלומר, זווית ACD = את הפינה של BCD ואת זווית ADC = פינת BDC. מכאן השוויון 1 כי CD הוא bisector. ואת הזווית ADC ואת זווית BDC הם זוויות צמודות, וזה נובע השוויון 2 כי הם שניהם ישר. מתברר כי תקליטור הוא גובה של משולש. זה המאפיין של החציון של משולש איסוסל.

ועכשיו קצת על הסימנים של משולש משקפיים.

משפט 3

אם במשולש שתי זוויות שוות זו לזו, אז משולש כזה הוא משקפיים

הוכחת המשפט.

נניח שיש לנו משולש ABC, שבוזווית CAB = פינת CBA. משולש ABC = משולש BAC על ידי הסימן השני של השוויון בין משולשים. אז זה, כי AB = BA; זווית CBA = זווית CAB, זווית CAB = זווית CBA. מן השוויון הזה של משולשים יש לנו את השוויון של הצדדים המקביל של המשולש - AC = BC. ואז מתברר כי המשולש ABC הוא שוהים.

משפט 4

אם בכל משולש כלשהו החציון שלו הוא גם גובהו, אז משולש כזה הוא שוהים

הוכחת המשפט.

במשולש ABC, אנו מציירים את חציון התקליטור. זה יהיה גם גובה. משולש מלבני ACD = משולש מלבני BCD, שכן התקליטור נפוץ עבורם, והקתודה AD = BD. מכאן נובע כי hypotenuse שלהם שווה אחד לשני, כמו החלקים המתאימים של משולשים שווים. משמעות הדבר היא כי AB = BC.

משפט 5

אם שלושת הצדדים של המשולש שווים לשלושת הצדדים של המשולש האחר, אז המשולשים האלה שווים

הוכחת המשפט.

נניח שיש לנו משולש ABC ומשולש A1B1C1 כך שהצדדים AB = A1B1, AC = A1C1, BC = B1C1. אנו רואים את ההוכחה של משפט זה על ידי סתירה.

נניח שהמשולשים האלה אינם שוויםבעצמך. לפיכך יש לנו את זווית BAC אינו שווה את זווית B1A1C1, זווית ABC אינו שווה את הזווית A1B1C1, ACB זווית אינו שווה את זווית A1C1B1 באותו זמן. אחרת, המשולשים האלה יהיו שווים בהתאם לתכונה הנ"ל.

נניח כי משולש A1B1C2 = משולשABC. במשולש, קודקוד C2 שוכב עם קודקוד C1 יחסית לקו A1B1 בחצי אחד המטוס. הנחנו כי הקודקודים C2 ו- C1 אינם חופפים. נניח שהנקודה D היא נקודת האמצע של C1C2. אז יש לנו משולשים isosceles B1C1C2 ו A1C1C2, אשר יש בסיס משותף C1C2. מתברר כי החציון שלהם B1D ו A1D הם גם לגבהים שלהם. משמעות הדבר היא כי קו ישר B1D ואת קו ישר A1D הם בניצב לקו ישר C1C2.

B1D ו- A1D יש נקודות שונות B1 ו A1, ולכן, לא יכול לחפוף. אבל למעשה, דרך נקודת D של C1C2 אנחנו יכולים לצייר רק שורה אחת ישר בניצב את זה. יש לנו סתירה.

עכשיו אתה יודע מה הם המאפיינים של משולש isosceles!