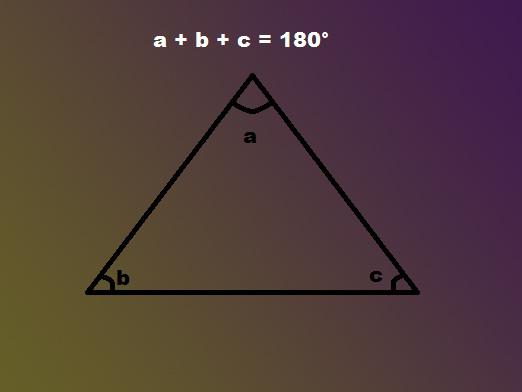
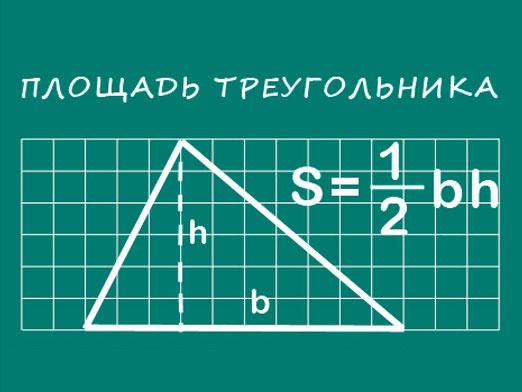
איך למצוא את הזוויות של משולש איסוסל?
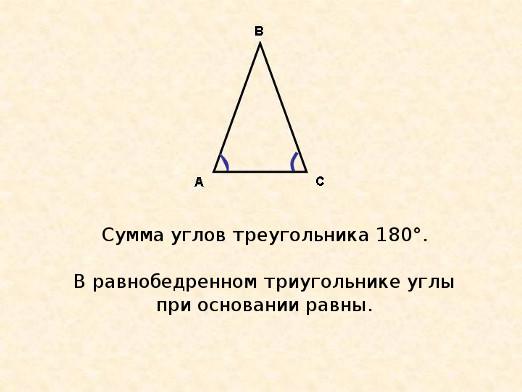
משולש משקפיים הואהמצולע הפשוט ביותר בעל שלוש זוויות ושלושה צדדים. לפני שאתה להבין איך למצוא את הזוויות של משולש isosceles, אתה צריך לדעת את המאפיינים של דמות גיאומטרית זו.
מאפיינים של משולש איסוסל
תן לנו לשקול את המאפיינים של משולש isosceles.
- במשולש איסכאלאס, שני הצדדים שווים. הצד השלישי הוא הבסיס.
- זוויות בבסיס משולש כזה שוות.
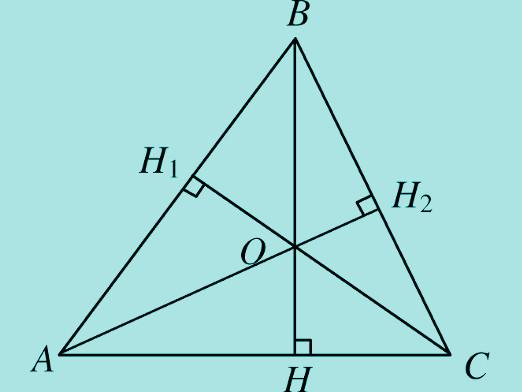
- Bisector, החציון ואת גובה נמשך מן הפינות אל הצד הנגדי של הדמות הגיאומטרית הם גם שווים.
- Bisector, חציון וגובה מן הפינה העליונה לבסיס המשולש isosceles חופפים.
- אם אתה רושם מעגל בתוך משולש משקפיים, ומתאר אותו סביב דמות כזאת, המרכזים שלהם ישכבו על אותו קו.
- הפינות בבסיס יכולות להיות חדות בלבד.
לכן, אם שתי זוויות שוות במשולש, וגובהו עולה בקנה אחד עם חציון ו bisector, זה isosceles. זהו הסימן העיקרי של משולש משקפיים.
עכשיו, שקול איך למצוא את הזוויותמשולש משקפיים. אם משולש כזה הוא גם מלבני, לא קשה למצוא שתי זוויות שלו, כך שהם תמיד יהיו שווים ל 45 מעלות, אשר בעקבות תכונות וסימנים של משולש isosceles.
- לדעת אחד הזוויות, אתה תמיד יכול לחשבהכרחי. לדוגמה, הזווית בבסיס תהיה מסומנת על ידי האות α, הזווית ב קודקוד של הדמות יהיה מסומן על ידי האות β. מכאן שזווית α תהיה שווה ל: (π - β) / 2, כאשר π הוא קבוע.
- זוויות יכול להיות מחושב גם מתוך arcsines. לשם כך יש צורך לתאר משולש כזה סביב המעגל עם רדיוס אשר כונה על ידי מכתב בה"א הידיעה ואז, הזווית α = arcsin (א / 2R), ואת זווית β = arcsin (b / 2R), שבו a ו- b הם הצדדים של משולש.
דוגמה לפתרון הבעיה
יש צורך למצוא את זוויות משולש isosceles אם ידוע כי הזווית בבסיס שלה הוא 15 מעלות יותר מאשר זווית כי הוא מול הבסיס.
פתרון: ציין את הזווית ההפוכה β, ולאחר מכן את הזווית בתחתית יהיה: β + 15. מאז הסכום במשולש הוא תמיד 180 מעלות, אנו מוצאים:
β + 2х (β + 15) = 180;
β + 2 β + 30 = 180;
3 β = 180-30;
3 β = 150;
β = 50
אז, את הזווית בתחתית הוא 50 מעלות, ואז שתי זוויות אחרות שווים 65 מעלות כל אחד. עכשיו אתה יודע את הכללים של איך למצוא את הזוויות של המשולש isosceles. אנו מאחלים לכם הצלחה בכל החישובים!