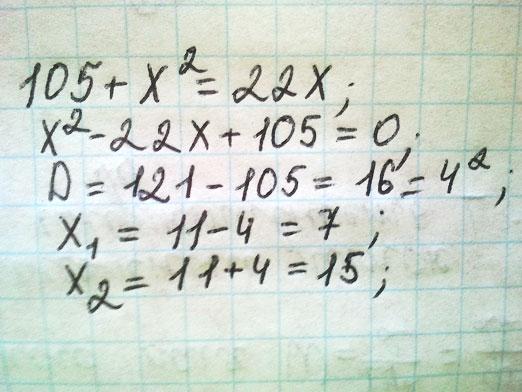כיצד לפתור את השורשים?

אני באמת לא אוהב כמה תלמידיםמשוואות ובעיות בהן מתרחש השורש. אבל זה לא כל כך קשה כדי לפתור את הדוגמה שורש, חשוב לדעת איזה צד לגשת לבעיה. הסמל עצמו, המציין את החילוץ של השורש, נקרא רדיקלי. כיצד לפתור את השורשים? חלץ את השורש הריבועי של המספר - זה אומר, להרים מספר בכיכר ייתן את אותו ערך תחת הסימן של הרדיקלי.
אז, איך לפתור את השורשים הריבועיים
פתרון שורשים מרובעים לא קשה. לדוגמה, אתה צריך לגלות כמה השורש יהיה מ 16. על מנת לפתור את זה פשוט, אתה צריך לזכור כמה יהיו 2 בתיבה - 22, ולאחר מכן 32, ולבסוף, 42. רק עכשיו אנו רואים כי התוצאה (16)מתאים לבקשה. כלומר, כדי לחלץ את השורש, היינו צריכים לבחור את הערכים האפשריים. מתברר כי על מנת לפתור את השורשים, אין אלגוריתם מדויק ואמין. כדי להקל על העבודה של "פותר", מתמטיקאים מומלץ לשנן (על ידי הלב, כמו לוח כפל) את הערכים של הריבועים של מספרים עד עשרים. אז אתה יכול בקלות לחלץ את השורש מן המספרים כי הם יותר ממאה. לעומת זאת, לראות מיד כי השורש של מספר זה לא ניתן לחלץ, כלומר, התשובה לא תהיה מספר שלם.
הבנו איך לפתור שורשים מרובעים. ועכשיו בואו להבין מה פתרונות שורש ריבועי אין. לדוגמה, מספרים שליליים. כאן ברור כי אם שני מספרים שליליים מוכפלים, התשובה מתקבלת עם סימן פלוס. יתר על כן, כי יש צורך לדעת. שורש ניתן לחלץ מכל מספר (למעט שלילי, כאמור לעיל). רק התשובה יכולה להפוך לחלק עשרוני. כלומר, להכיל מספר מסוים של ספרות לאחר הנקודה העשרונית. לדוגמה, השורש של שני יש את הערך 1.41421 וזה לא כל הספרות אחרי הנקודה העשרונית. ערכים אלה מעוגלים כדי לאפשר חישובים, לפעמים לספרה השנייה לאחר הפסיק, לפעמים השלישי או הרביעי. בנוסף, הוא התאמן לעתים קרובות להשאיר את המספר תחת השורש כתשובה אם זה נראה טוב קומפקטי. זה כל כך ברור מה זה אומר.
איך לפתור משוואות עם שורשים?
על מנת לפתור משוואות עם שורשים יש ליישם אחת מהטכניקות שלא המציאנו. לדוגמה, להעלות את שני הצדדים של משוואה כזו לריבוע. לדוגמה:
שורש X + 3 = 5
הבה נמתח את צד שמאל ומשמאל של המשוואה:
X2 + 9 = 25
עכשיו אתה יכול לראות איך לפתור את המשוואה הזאת. ראשית אנו לברר מה X שווה2 (וזה שווה ל 16), ואז אנו לחלץ את השורש ממנו. תשובה: 4. עם זאת, כאן כדאי לומר כי משוואה זו למעשה יש שני פתרונות, שני שורשים: 4 ו -4. אחרי הכל, -4 בכיכר גם לתת 16.
בנוסף לשיטה זו, לפעמים זה יותר אטרקטיבי ונוח להחליף משתנה כי הוא מתחת לשורש - משתנה נוסף, כדי להיפטר השורש הזה.
Y = שורש X.
לאחר מכן, בפתרון המשוואה, אנו חוזרים להחלפה ומסיימים את החישובים עם השורש.
כלומר, אנחנו מקבלים X = Y2. וזה יהיה הפתרון.
יש לומר כי ישנן מספר שיטות לפתרון משוואות עם שורשים.
כיצד לפתור את השורשים תואר?
הרדיקלי, שבבסיסו אין תואר,אומר שאתה צריך לחלץ את הביטוי או מספר השורש הריבועי, כלומר, את הריבוע ולהיפך. זה פשוט ומובן. לדוגמה: השורש של 9 = 3, (3)2 = 9), השורש של 16 = 4 (4)2 = 16) וכולם באותה רוח. אבל מה זה אומר אם שורש יש תואר? משמעות הדבר היא, כי שוב, יש צורך לבצע פעולה נגד הקמתה במידה זו מאוד. לדוגמה, אתה צריך לדעת את הערך של השורש של מעוקב של 27.
לשם כך, יש לבחור מספר, כאשר הקימו בקוביה, ייתן 27. זהו 3 (3 * 3 * 3 = 27).
לפיכך:
שורש 3 מתוך 27 = 3
פעולות דומות יש לבצע אם מידת השורש הוא 4, 5. רק במקרה זה יש צורך לבחור מספר אשר, כאשר הרים את הכוח n ייתן ערך מתחת לשורש nתואר
כאן יש צורך לומר כי מעלות השורשים ואת התוארביטויים כפופים ניתן לצמצם. עם זאת, על פי הכללים. אם למספר או למשתנה מתחת לשורש יש תואר שהוא מספר של דרגת השורש, ניתן לקצר אותם. לדוגמה:
שורש3 מ X6 X = X2
כללי פעולה אלה עם שורשים מעלות הם פשוטים, אתה צריך לדעת אותם בבירור, ולאחר מכן החישוב יהיה פשוט. איך לפתור את השורשים תואר, הבנו, עכשיו אנחנו ממשיכים הלאה.
כיצד לפתור את השורש מתחת לשורש?
זה ביטוי נורא של השורש מתחת לשורש בהתחלהמבט שלא ניתן לפתור. אבל כדי לחשב נכונה את הערך של ביטוי כזה, אתה צריך לדעת את המאפיינים של השורשים. במקרה זה, אתה רק צריך להחליף שני שורשים - אחד. לשם כך יש להכפיל את מידת הרדיקלים האלה. לדוגמה:
שורש3מהשורש 729 = (שורש3* root2) של 729
כלומר, כאן הכפלנו את שורש הקובייה לשורש הריבועי. כתוצאה מכך, השגנו השורש השישי:
שורש6 מתוך 729 = 3
כמו כן, יש צורך לפתור שורשים דומים אחרים תחת השורש.
לאחר שקל את כל הדוגמאות המוצעות, זה קללהסכים שפתרון השורשים אינו משימה כה קשה. כמובן, כאשר זה מגיע אריתמטית פשוטה, בנאלית, לפעמים זה יותר קל להשתמש במחשבון הרגיל. עם זאת, לפני ביצוע החישובים, אתה צריך לעשות הכל כדי לפשט את המשימה על ידי צמצום מספר ומורכבות של חישובים אריתמטיים. אז הפתרון יהיה פשוט, והכי חשוב, מעניין.