איך מספרים עגולים?

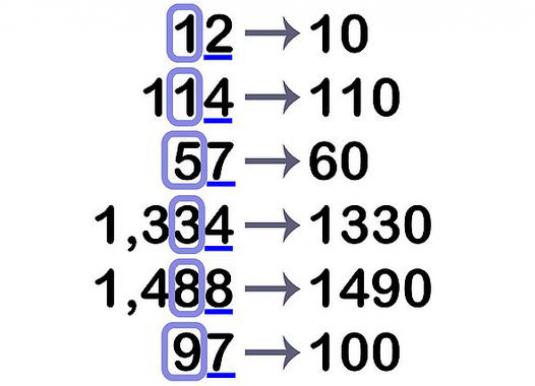
מספרי העיגול הם הפעולה המתמטית הפשוטה ביותר. כדי להיות מסוגל מספרים עגולים כראוי, אתה צריך לדעת שלושה כללים.

תקנה 1

כאשר אנו מעגל מספר לרמה מסוימת, אנחנו חייבים להיפטר מכל הספרות משמאל דרגה זו.

לדוגמה, אנחנו צריכים לסובב את מספר 7531 עד מאות. במספר הזה חמש מאות. מימין לספרה זו יש מספרים 3 ו -1. אנו הופכים אותם לאפסים ומקבלים את המספר 7500. כלומר, מעגל המספר 7531 למאות, קיבלנו 7500.

כאשר מעגל את מספרי השבר, הכל קורה כךרק ניתוחים מיותרים יכולים פשוט לרדת. נניח שאנחנו צריכים לסובב את מספר 12.325 לעשירית. כדי לעשות זאת, לאחר פסיק, אנחנו חייבים להשאיר ספרה אחת - 3, ואת כל המספרים בצד ימין, להשליך. התוצאה של עיגול המספר 12.325 לעשירית היא 12.3.

כלל 2

אם הספרה שהושלכה מימין לספרה השמאלית היא 0, 1, 2, 3 או 4, אז הדמות שאנחנו משאירים אינה משתנה.

כלל זה עבד בשתי הדוגמאות הקודמות.

אז, כאשר מעגל את מספר 7531 עד מאות עצמוקרוב למספר שנותר מן המושלך היה משולש. לכן, הדמות שעזבנו - 5 - לא השתנתה. תוצאת העיגול היא המספר 7500.

באופן דומה, כאשר מספר מעוגל את 12,325 להספרה העשירית, שהורדנו אחרי השלושה, היתה שתיים. לכן, הימנית של ספרות שמאל (משולש) לא השתנה בעת עיגול. זה היה 12.3.

כלל 3

אם השמאלה של הספרות שהושלכו שווה ל 5, 6, 7, 8 או 9, אז הספרה אליה אנו מעגל הוא גדל על ידי אחד.

לדוגמה, אתה צריך לסובב את מספר 156 עד עשרות. במספר זה של 5 עשרות. בקטגוריה של יחידות, שממנו אנו הולכים להיפטר, יש דמות 6. לכן, את עשרות ספרות צריך להיות מוגדל על ידי אחד. לכן, כאשר מעגל את מספר 156 עד עשרות, אנחנו מקבלים 160.

שקול דוגמה עם מספר חלקי. לדוגמה, אנחנו הולכים סביב 0.238 למאות. על פי הכלל הראשון, עלינו להוריד את השמונה, שעומדת מימין לכיתה י"א. ועל פי הכלל 3, נצטרך להגדיל את שלושת הראשונים במאה אחד על ידי אחד. כתוצאה מכך, מעגל את מספר 0.238 למאות, אנחנו מקבלים 0.24.